Understanding Convexity Risk: From Bonds to Options
In the complex world of finance, understanding convexity risk is crucial for both bond and options traders. This article synthesizes insights on convexity risk, focusing on its implications for investors and providing real-world examples that illustrate these concepts.
What is Convexity Risk?
Convexity risk refers to the potential for bond prices to change rapidly in response to fluctuations in interest rates. This relationship is characterized by a convex curve, meaning that as interest rates rise, bond prices typically fall, but not in a linear manner. Instead, the changes in price can accelerate, leading to significant principal risk for bondholders.
The Inverse Relationship Between Bonds and Interest Rates
Bonds exhibit an inverse relationship with interest rates: when rates rise, bond prices fall, and vice versa. This fundamental principle creates convexity risk. However, many investors do not fully grasp the implications of this relationship. As one expert noted, "When you tell people to buy bonds, they really don't understand that there's principal risk." This lack of understanding can lead to complacency among investors who focus solely on the guaranteed interest payments offered by bonds.
Principal Risk: A Hidden Danger
Investors often approach bonds with a false sense of security. They may believe that because they are receiving interest payments, their investment is safe. However, they frequently overlook the risks associated with changes in interest rates. The conversation highlights that while stock investors are acutely aware of potential losses—"the first thing that people think when you say you should buy a stock is how much money can I lose"—bond investors may not consider principal risk until it’s too late.
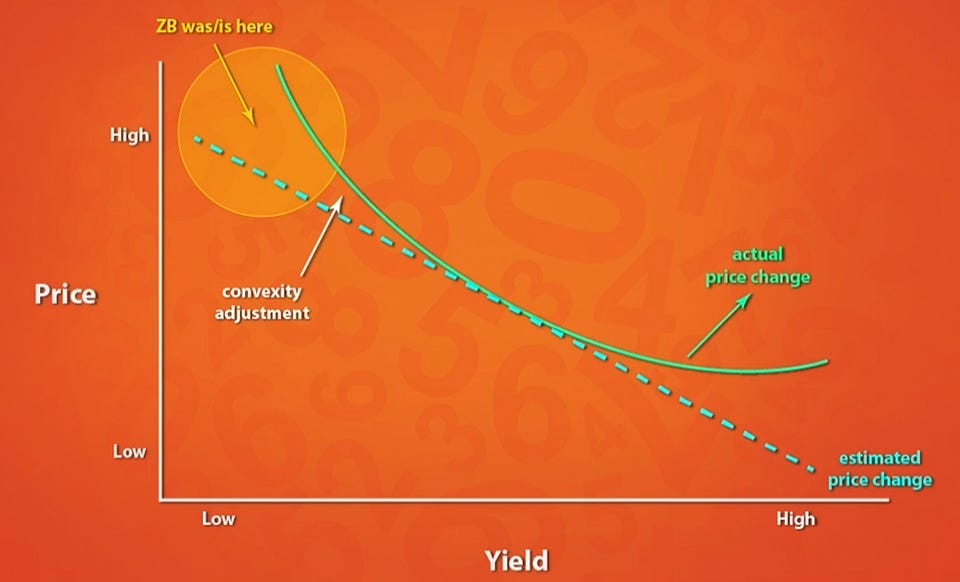
Graphical Representation of Convexity Risk
To visualize convexity risk, consider a graph with price on the y-axis and yield (or interest rates) on the x-axis. The relationship appears as a downward-sloping curve. While many formal equations depict this relationship as linear (represented by a dashed line), the actual price changes follow a convex curve. This curvature indicates that as bond prices drop from high levels, they do so at an accelerating rate.
For example, when bonds were trading at high prices (around 177), traders recognized they were in a precarious position. As one commentator noted, "When bond prices do drop... they're anticipated because of the convex relationship to drop very, very quickly." This accelerated principal risk is particularly concerning for those who do not fully grasp its implications.
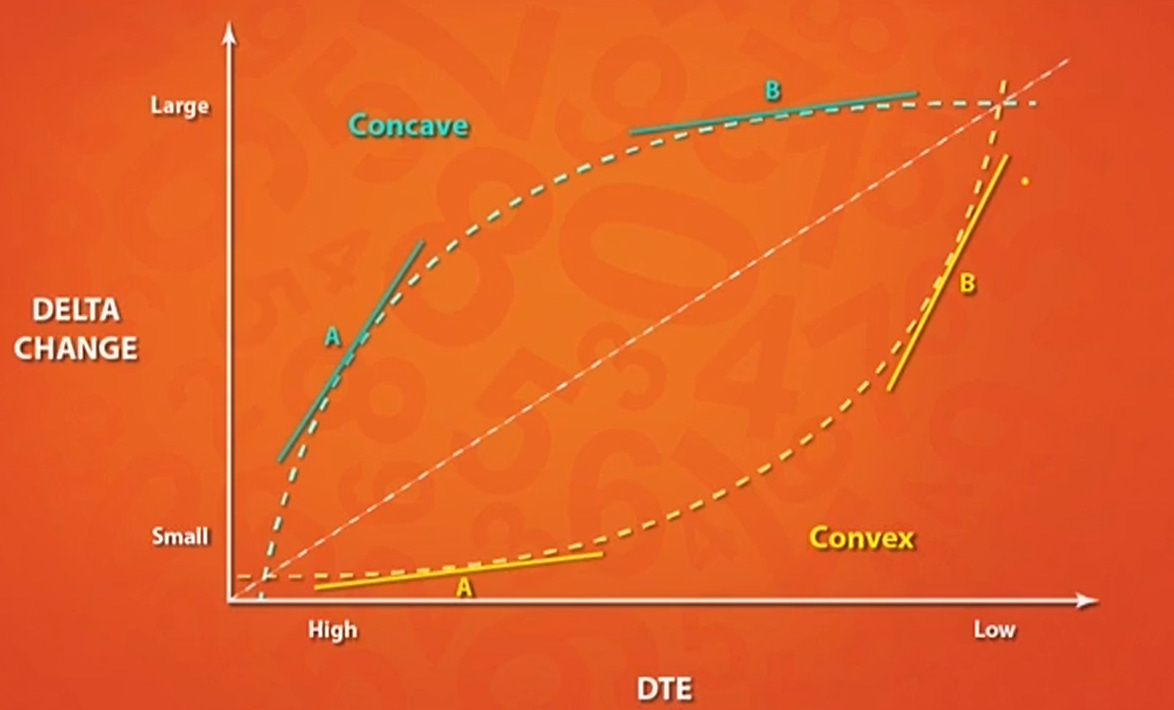
Transitioning to Options: Understanding Gamma and Delta
We shift our focus from bonds to options. Just as bond traders must be aware of convexity risk, options traders face similar challenges due to gamma's relationship with delta. Gamma measures how much an option's delta (the rate of change of an option's price concerning changes in the underlying asset's price) will change as the underlying asset's price changes. This connection between gamma and delta mirrors the convex relationship observed in bonds. As options traders navigate their positions, understanding how these dynamics play out can help them manage risks more effectively.
Real-World Examples: The Impact of Convexity Risk
Bonds at High Prices: When bond prices were at 177 with yields at 0 or negative levels, traders faced significant convexity risk. If they held these bonds and prices began to drop, they would experience accelerated losses due to the steep slope of the convex curve.
Options Trading: In options trading, understanding gamma is essential because it can lead to rapid changes in delta. For instance, if an option holder is near expiration and market conditions shift quickly, their position could deteriorate faster than anticipated due to gamma's influence.
Market Anticipation: Market anticipation can affect bond prices. For example, if traders expect an interest rate hike and prices adjust accordingly before it happens, the actual hike may not lead to expected drops in bond prices because the market has already "baked in" those expectations.
Key Takeaways
Bonds as Central Portfolio Assets: Bonds play a crucial role in diversified portfolios due to their liquidity and low correlation with equities. However, their unique relationship with interest rates exposes them to convexity risk.
Awareness of Principal Risk: Investors must recognize that while bonds offer guaranteed interest payments, they also carry significant principal risk that can lead to accelerated losses when market conditions change.
Cross-Asset Insights: The principles of convexity risk extend beyond bonds into other asset classes like options. Understanding these relationships can enhance overall investment strategies.
Education is Key: Both bond and options traders benefit from education about convexity risk and its implications for their portfolios. Recognizing these dynamics can lead to more informed decision-making and better risk management.
Conclusion
As we explore the complexities of convexity risk across different financial instruments, it becomes clear that understanding these concepts is essential for all investors. Whether dealing with bonds or options, awareness of how price movements relate to underlying risks can significantly impact investment outcomes.
By fostering a deeper understanding of convexity risk, investors can navigate financial markets more confidently and strategically. Whether you're trading bonds or options, recognizing these dynamics will empower you to make informed decisions that align with your financial goals.
In summary, whether you're looking at bonds or options trading strategies, understanding convexity risk—and its manifestations—can provide critical insights into managing your investments effectively in an ever-changing market landscape.